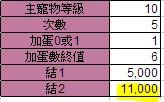
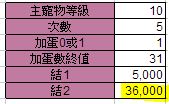
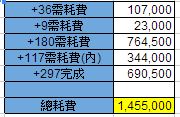
但要注意的是,這裡完成+31的耗費,不包括5次的完成+6耗費,
也就是說你要完成一隻+31的寵,你還得加上5倍單次完成+6耗費;
這裡以完美的(實際上並不簡單)的LV10寵當基底,
(P.S.:為了避免誤解,所以補充──打到的+蛋寵,幾乎都會低於LV10;
也就是說,基本上這個↓理想值是絕對會比實際情況還要貴的。)
我們得花費『91,000』(=(11,000*5)+36,000)
才能完成一隻+31的寵。
(懶人包指引#3)
雖然看起來很理所當然,但其實又有點莫名其妙?
但如果有認真看、思考的讀者,或許馬上就遇上一個困境:
「為什麼要用+1的寵物當底,而不是+6的?」
如果你還記得前面我們說過的:
『最好減少「寵物最終+蛋數值」的總合;』←這句話,
前頭也有說到,就像是堆疊金字塔一樣的感覺;
也就是說,如果用+6的寵當底,
當再用5個+6寵,讓它加到+36時,
我們就得要在多付一次基底那隻+1~+6的金額。
而我們從最初的目的,就是要想盡辦法減少這筆錢。
或許一開始是一筆小數目,
但如果你得累積非常多個+36時,
這數目就會變成龐大的差距,
讓你得多花了些冤枉錢。
(文末稍微詳細解釋)
---------------------休息分隔-----------------------
Part 2. 最大利益獲得+297?格子?金錢?
如果你發現你搞清楚Part 1在做什麼了,
那麼你已經可以省下一筆不必要的負擔了。
但如果你還是懵懵懂懂、不知這傢伙所云,
那也沒關係,因為這Part 2會比較詳細的解釋一些要因。
不囉嗦,首先大家最關心的一定是+297的方法。
當然這也是這篇文章的核心問題,
所以筆者就直接以結論做為開頭:
利用9個+31的寵與一隻+18的寵物,
分別以+155→+297的兩次行程,
讓你想要+297的寵物達成這個目標。
好像有聽沒有懂?沒關係,因為筆者也不知道自己在寫什麼。
嘛,首先我們該做的是利用上一段理解的內容,
以直覺的反應來想就是:
一次餵五隻+31的寵物,會讓我們省掉每次多額外增加的負擔。
所以首先我們該做的就是,
首個行程,一次將5隻+31的寵物,
毫不手軟地吃下去!
(懶人包指引#4)
這裡要注意的是,如果你的愛寵本身就有(少量)+值時,
會稍微改變最終耗費的金額,但並不會影響太多。
而那個差值,我們在後文會再提起,有個印象就行。
第一個行程結束時,
你的愛寵理想的加值應該是+155,
但在第二個行程前,我們要注意的一個重點是:
「再餵遍5隻+31的話,我的寵物就超過+297了啊!」
沒錯,所以如果讀者您還記得,本文一開始所提到的內容的話。
我們要準備的是9隻+31的寵與1隻+18的寵。
所以我們第二個行程,
就變成餵剩下的4隻+31寵外加1隻+18的寵。
(懶人包指引#5)
如果你數學比筆者好一些,就算不拿出計算機,
我想你馬上就會發現,你的寵物剛剛好+滿值了。
那麼恭喜你,其實此篇的核心問題已經到此結束了。
雖然很想不負責任地就這樣交差了事,
簡言之,如果你照這上頭的兩個行程做,
應該會遇到的兩個比較嚴重的困境,
但在解釋問題之前,
依照慣例我們得先拿出證據來。
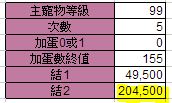
第一個行程:
第二個行程:
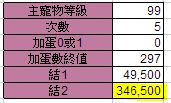
但前半的模式,這兩張圖所代表的是該次合成所耗費的金額,
並不包括得到5個+31(與4個+31和1個+18)所耗費的金額。
也就是說兩行程實際耗費的金額是:
=659,500 (=(91,000*5)+204,500)
和
=764,500(=(91,000*4)+54,000+346,500),
(↑其中的54,000是+18所要耗費的金額。)
而終於到最後了,
我們所獲得的總花費額就是這兩個數字的總合。
也就是:
=1,424,000。
(懶人包指引#6)
也許你沒什麼感覺
但這確確實實是最省錢的方法之一!
在沒有比較的情況下,這個數字是相當萌稜兩可的,
不過這個數字您先記得就好,
因為我們得先解決另外幾個比較嚴重的問題。
---------------------休息分隔-----------------------
Part 3. 常見問題。
休息片刻後,我們來說說上一段最後所講到的,
我們比較會面臨到的幾個問題吧。
Q1:我該怎麼做,才不會三圍加值超過+99,
而多浪費了加蛋呢?
這個問題其實相當好解決,但也是最麻煩的部分;
唯一沒有第二種方法,那就是土法煉鋼一個一個算。
但因為我們會獲得9隻+31的寵物,
所以你可以試著將不同的三圍,
分別餵個不同的三組寵物,
如果你怕忘記或看錯,
你甚至可以特地去抓三色波利來代表各個屬性。
而這個問題馬上會遇到的新的困境,
如果我的愛寵,一開始就有加值呢?
(或是你不小心餵了個+1X)
這個困境看起來與前面那個沒什麼關係,
但解決的辦法卻是雷同的。
如果你還記得第二個行程中,
我們最後一隻寵物並不是用+31的話,
那麼你可能已經找到解答了。
在我們訂做第10隻寵物的時候,
你就可以試著微調與本身值互補的加值。
當然如果你的愛寵是+0,
這隻+18的寵物加值的三圍,
理想必定該是6、6、6。
如果不是或超過的話,
那麼你得小心多吃所浪費的加蛋,
與多補一顆所要耗費的金額了。
(多補一顆就是從+296~+297所要耗費的金額,
將近30w並不是小數目,所以再計算加值時切記要謹慎。)
而第二個問題是大家比較關心,而且甚為重要的:
Q2:我的格子好像不夠,該怎麼辦?
當然土豪會跟你說,那就多開幾個啊!
當你存的素材、隊伍越多,
你就得要以倍數成長的來增加格子,
才能負擔大量的寵物。
但此種分配+值模式,並不會太大量地消耗你的格子數;
實際上它或許比你想像中的還要省格子多了。
首先我們得先注意到一點,那就是:
兩個行程是分開的。
施主,先別衝動,放下手中的凳子。
如果你有瞬間靈機一閃、茅塞頓開、恍然大悟的感覺,
那麼你大概知道我想說什麼了。
你只要累積5個+31的寵物,
就可以馬上將它加到你的愛寵上。
而不需要等到累積滿9+1隻,
再一次進行兩個行程。
這段話很白痴,我知道。
但卻代表了很多事情。
一、你不需要扛著+0的愛寵到打滿297(應該會超過)加蛋,
途中第一次的加值,就能讓你的愛寵有不少威力的提升。
而甚至你可以挑選特別的三圍(HP特化、攻擊特化etc.)的情況。
畢竟297顆加蛋不是說打就打的到的,
這其中你總會想要打些別的東西吧?
而提前第一次行程的+155,無疑是提升不少寵物的能力。
二、這就表示你可以省下不少格子,
來堆放那可恨又可愛的+蛋寵了;
而實際上到底可以、需要多少額外格子才能達成這項任務呢?
我們先來想想最佳的情況吧:
你已經有了4隻+31、5隻+6、1隻愛寵,
而他們的加值是最佳的理想值,
所以忽略掉任何三圍的影響。
在這個亂七八糟有聽沒有懂的條件下,
你所需要額外的格子只要:
4格+31、5格+6、1格愛寵、
1格將會打到的且你需要的加蛋;
也就是說你只要額外留著11格(包括愛寵),
你就能完成一次最理想的行程。
也許是令人驚訝的數字,但理想總是理想,
掉加蛋不可能想要什麼就來什麼;
所以這是最小值,那麼我們該思考的就是最大值是多少。
而真正花費格子的情況會存在於第二次行程,
不過我們還是得要先理解多餘花費的困境在哪。
當然情況就會發生在當我們擁有了
5隻+1的攻擊、5隻+1的HP、5隻+1的回覆蛋時。
為了要讓我們的+6是保持同樣的一種屬性,
最糟糕的情況就是三圍都擁有了5隻,
但這也表示我們不管在打到任何的加值寵,
都能獲得一隻+6寵。
而相同的概念,我們也有可能會獲得同時獲得
5隻+6的攻擊、5隻+6的HP、5隻+6的回覆蛋。
不過與前段相同的是,我們只要再獲得任何一顆+1的蛋,
不論如何都能再獲得一隻+31的寵了。
所以從基本邏輯來推理,
我們要獲得一隻+6的寵,最糟糕的情況就是要有16額外的格數。
而我們要獲得一隻+31的寵也是相同的情況;
但是我們要製造+31的蛋寵,最後需要的是一顆+1的蛋,
所以不會變成單純進位的情況。
也就是說當我們遇上:
情況一:
4格+31、1格愛寵,
5隻+6的攻擊、5隻+6的HP、5隻+6的回覆蛋
一隻隨意三圍的寵物。
總計21格。
這情況是建立在不論(理想)前面四隻+31的情況下,
而我們得要再獲得任意一隻加值才能進位獲得最後一隻+31寵;
當然這個條件算是比較簡單的,
一方面也是為了要建築出下一個條件。
情況二:
4格+31、1格愛寵,
5隻+6的某某、5隻+6的某某、4隻+6的某某蛋,
5隻+1的攻擊、5隻+1的HP、5隻+1的回覆的前提下;
必須再打到3隻不同加值+1。
總計至少37格。
這種情況下就突然複雜許多了,
除了情況一的限制下,我們還多出了個條件:
「當我們還缺了一隻+6的情況下。」
所以在逆理想情況下,我們得至少收集三圍各一隻,
才有辦法獲得最後一個+6。
不過要注意的是在這種情況下,獲得最後一個+6之後,
我們還會剩下多兩顆+1,
所以能夠拿其中一顆再做出最後一隻+31,
而完成一次行程後,我們仍會多出一格+1。
(要注意的是,我們打到的任意加值,
都能夠讓其中一組+6被製造出來,
但此時我們就會再多出四格──無限Loop;
所以倘若你永遠打不到想要的那個值,
理論上當然是不管有多少格數都是不夠的。)
其實我們會發現,
理想的情況下,確實不太需要龐大的格子數量。
但有可能會因為有某個值的加蛋有非常多,
但是某個值的卻非常少。
雖然總值到了+297,卻不是三個+99
造成需要非常多的格子來堆放進位用的寵。
以理想的角度來說,11~37格是基本的範疇;
那麼最最最糟糕的情況呢?
其實這個數值是無限大的,
因為如果你永遠都打不到你缺的+1;
那麼就算你開滿了格子,你也絕對不夠的。
因此,以三圍加蛋掉落率是趨近同值的情況下,
那麼筆者還是建議有額外30左右的數量比較充足及保險。
但如果你是一個準備追求+297的玩家,
我想多空出個30格並不是什麼困難的問題;
甚至該是相當簡單的事。
Q3:為什麼我該聽你們的話,
照這個辦法去+297呢?
誰知道這些數據是不是唬洨的?
其實這個問題才是整篇文章的最大的難題,
也是筆者與朋友不斷問自己的一個問題:
「為什麼我們該這樣做呢?」
第一個目的當然是省錢,所以我們找了幾個其他的方式來反駁自己。
Qa:給我一個用這個方法比較好的理由。
Aa:這個問題看起來很單純,實際上也真的很單純。
但為了避免浪費太多篇幅在說廢話,
所以我決定用一張表格來輔助解釋。
如果你覺得怪怪的,或是少了不少東西,那是因為我把它隱藏了。
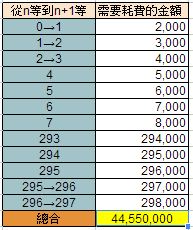
這張表格代表的意義很簡單,
就是你只花兩格的情況下,每打到一顆加蛋,就拿去餵給你的愛寵一次;
當你餵到+297時的所耗費的總金額。
因為圖太小,所以我把它寫出來放大以便觀察:
=44,550,000
如果你忘記了我們內文,所得出的答案是多少的話,
沒關係!
我在複製貼上一次給你看。
=1,424,000
看起來差不多啊?都有很多個0(被打
我知道你會覺得拿出計算機太麻煩,
所以我替你先算出了它們的差額。
=43,126,000
Qb:難道沒有其他的方法嗎?
比如說用+36的加蛋寵時,結果會發生什麼事情呢?
Ab:
這個問題比起上個問題,解釋來的簡單了一點。
因為我們只要找出其他方法的解,
來比較之間的多寡就行了。
過程有點繁瑣,所以就省略了。
這個方式與內文非常相似,
差別只在我們用的是6顆+6蛋合成+36,
而不是用5顆合成+31。
剩餘的步驟就和內文大同小異了。
大至為→累積8顆+36與1顆+9加蛋→分兩次餵滿+297。
結果的數值是
1,455,100
其實已經相當接近內文的金額了,
但是仍就差了那麼一點點。
P.S.:實際上本文內的方法已經確定不是最便宜的方式了。
在樓下也有其他版友提出類似的方法,但更便宜的模式;
所以方法還是因人而變的,沒有所謂的絕對。
Qc:是否總合成次數越少,所耗費的金額就一定越少呢?
Ac:答案是不一定的。
實際上還是要看「寵物最終+蛋數值」的總值,
當這個總值越高時,花費金額越貴的機會就越高;
並且數目越大,越和次數沒有絕對關係。
這邊利用上面用過的數據來稍作解釋:
情況一、當累積9隻+31與1隻+18的情況下。
1隻+6需要合成1次。
1隻+31需要合成1次,加上合成5次的+6,也就是6次。
9隻+31需要合成9次,加上每次合成的6次,也就是63次。
1隻+18需要合成1次,加上合成3次+6,也就是4次。
最後還需要花2次才能完成+297,
總共花的次數是63+4+2=69次。
花費金額為:1,424,000
情況二、當累積8隻+36與1隻+9的情況下。
1隻+6需要合成1次。
1隻+36需要合成1次,加上合成5次的+6,也就是6次。
8隻+36需要合成8次,加上每次合成的6次,也就是56次。
1隻+9需要合成1次,加上合成1次+6,也就是2次。
最後還需要2次才能完成+297,
總共花的次數是56+2+2=60次。
花費金額為:1,455,100
我想應該不用在計算差距了吧(?)
Qd:為什麼我最後實際的花費,比文內的結論還要便宜呢?
Ad:雖然大部分的人不會去在意這個問題,但被人問到還是要解答一下XD"
實際上,在前文也有提到:
「我們打到的加蛋,幾乎都是低於Lv10的寵物。」
而除了最後一次給愛寵吃的機會以外,
我們每一次都是以+1的寵物當底,
而這個+1的寵絕對不會再當底一次。
也就是說,除非你採用的是+36的模式,
不然,其實
你不太需要在意你當底的那隻的等級。
這也是為什麼此文採+31,而不是++36的原因之一。
不過,其實那點小錢實在不太需要在意XD"
所以,如果你花的錢比此文算出來的還要少的話!
請當作撿到賺到吧XDD
----------------------------------文末分隔-----------------------------------
也許除了內文之外,還有更佳的方法,
只是以筆者與朋友的小腦袋,
似乎還沒有想出更好的辦法、更好的結果;
如果您有特別的想法,也歡迎提出來讓我們嘗試。
當然,雖然是數據流的形式,且您也花時間看完這篇文章了,
但還是要明確的告訴您,要達成一隻+297的寵物,
實際上,有九成以上的時間都是在反複刷無聊關卡,
耐心才是最重要的因素。
而這份計算只能做為參考利用,
你可以有更靈活、或是比較懶的利用方式。
畢竟能刷完297顆加蛋,
這其中獲得的金幣量也是不容小覷的。
也許不用那麼斤斤計較、吹毛求疵,
數據永遠都是死的,
請別太過苛責自己的腦袋與挑戰自己的耐心。
有時候就算多花了點錢,
但是省了不少時間也是一項不錯的選擇。
以上,如果還有什麼問題是我們沒想到的,
歡迎以留言或回應的形式告知我們。
如果有數據上的錯誤、問題,也非常歡迎且懇請各位指謫。
另外附上計算的試算表,
如果有興趣的朋友可以看看挑挑錯。
以上所有的數據都是從裡頭來的。
"Google、試算表:加蛋計算。"
---------------------全文完分隔線-------------------
懶人包:
Step1:
以最低等的+1寵為底,
每一次都塞滿+5為目標。
會獲得一隻+6的寵。
Step2:
依然以+1寵為底,
以塞滿5隻+6的寵為目標,
能獲得一隻+31的寵。
最終至少需要9隻+31的寵;
而為了避免超額,
我們得額外做出一隻+18的寵物。
Step3:
以5隻+31的寵、4隻+31與1隻+18的寵,
分2次,餵給你的愛寵,
切記要注意加量的總值,
以免超過單一數值+99。
END
 弧角遮罩
弧角遮罩